

Therefore, in 1921, he revised his argument for the aprioricity of geometry as stated in 1910. Cassirer emphasized that the geometrical hypotheses of general relativity differed completely from those of Newtonian mechanics and of special relativity. While most of the large-scale evidence points to a Euclidean structure, there is some tantalising evidence that we might just live in a hyperbolic world.This chapter gives a brief account of the debate about the foundations of geometry after general relativity, with a special focus on Cassirer’s view in 1921. One of the major questions astronomers are trying to resolve, with instruments such as the Hubble Space Telescope, is what shape our universe has. Galileo Galilei and Isaac Newton founded modern physics on the assumption that space is Euclidean, but Albert Einstein’s equations of general relativity describe a universe that can have complex curved forms. Once mathematicians realised that different geometrical spaces are possible, a question arose as to which one is realised in physical space. More than 8,000 women in a dozen countries (including Australia, the United States of America, and the United Arab Emirates) have participated in making these installations, which reside at the intersection of mathematics, marine biology, community art practice and environmentalism. Here, a ball of wool and a crochet hook become pedagogical tools bringing mathematics out of textbooks, and taking it to people as a living tactile experience.
Non euclidean geometry art how to#
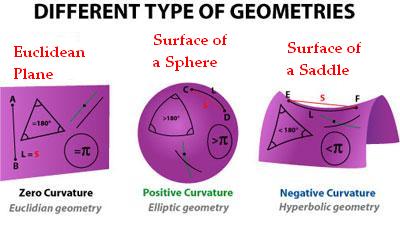
That year Cornell mathematician Daina Taimina also worked out how to model such surfaces using crochet, which was a big deal because it’s actually hard for humans to construct these forms.Ī crochet coral reef based on hyperbolic geometry. These carbon nano-foams were discovered in 1997 by physicist Andrei Rode and his colleagues at the Australian National University. Hyperbolic surfaces can also be built at the molecular scale from carbon atoms. In the film Avatar, there is a fabulous CGI grove of giant hyperbolic blooms that curl up when touched. There are hyperbolic structures in cells, hyperbolic cacti and hyperbolic flowers, such as calla lilies. Wherever there is an advantage to maximising surface area – such as for filter feeding animals – hyperbolic shapes are an excellent solution. Along with corals, many other species of reef organisms have hyperbolic forms, including sponges and kelps. Yet critters who’d never studied non-Euclidean geometry had meanwhile just been doing it. “For God’s sake please give it up,” said the Hungarian mathematician Wolfgang Bolyai to his son János Bolyai, urging him abandon to work on hyperbolic geometry. When mathematicians discovered this aberrant geometry in the early 19th century they were nearly driven mad. It’s a geometric analogue of a negative number. The surface of a sphere (like a beach ball) has positive curvature, and a hyperbolic plane has negative curvature.

A flat, or Euclidean plane has zero curvature. One way of understanding different geometries is in terms of their curvature. Margaret Cagyle, Institute For Figuring, Author provided All the pencil lines that appear to be curved were drawn with a ruler so they are actually straight. This image shows straight lines drawn on a paper model of a hyperbolic plane. And that, in turn, led to the revolution that produced the kind of maths now underlying general relativity, and thus the structure of the universe. Yet while nature has been playing with hyperbolic forms for hundreds of millions of years, mathematicians spent hundreds of years trying to prove that such structures were impossible.īut these efforts led to a realisation that hyperbolic geometry is logically legitimate. In hyperbolic geometry the plane is not necessarily so flat. These organisms are biological manifestations of what we call hyperbolic geometry, an alternative to the Euclidean geometry we learn about in school that involves lines, shapes and angles on a flat surface or plane. Yet outside our boxes, nature teams with frilly, crenellated forms, from the fluted surfaces of lettuces and fungi to the frilled skirts of sea slugs and the gorgeous undulations of corals. We have built a world of largely straight lines – the houses we live in, the skyscrapers we work in and the streets we drive on our daily commutes.


 0 kommentar(er)
0 kommentar(er)
